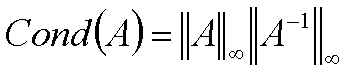To make the point of how inefficient it is to find the determinant of a matrix by the cofactor method, I wrote a program in MATLAB to demonstrate this. A google search for a program written in any language to find the determinant by using the cofactor method was not available beyond a 4×4 matrix. So, I wrote one that finds the determinant of matrices of up to 12×12 order.
I ran the program on an Intel(R) Core(TM) i5-8500 CPU @3.00GHz PC. Here is a table of the CPU time it took in seconds to find the determinant of a matrix as a function of its order.
______________________________________
Order of matrix CPU Time to Find
Determinant (s)
______________________________________
6×6 0.015625
7×7 0.046875
8×8 0.203125
9×9 0.828125
10×10 5.14063
11×11 52.6406
12×12 623.953
______________________________________
If one continues to do this for a 25×25 matrix, it is estimated that it would take 8.1821198 \times 10^{17} seconds which is more than 25 billion years, and we all know that the estimated age of the universe is less at about 13.77 billion years.
The trend of the approximate time it takes to find the determinant of the next order of the matrix, nxn is approximately n times the time it takes to find the determinant of a (n-1)x(n-1) matrix. For example, it took a time of 52.6406 seconds for finding the determinant of a 11×11 matrix, while it would be estimated to take approximately 12×52.6406=631.7 seconds for finding the determinant of a 12×12 matrix. This is close to the 623.953 seconds it actually took.
The above approximate time calculations are in concurrence with the note written by Professor A.J. Wise in 1969, where he showed that the number of arithmetic operations required to evaluate a nxn determinant by cofactor method is given by [n!e]-2, and hence n!e for large n and the time it takes to find the determinant of the next order of the matrix, nxn is approximately n times the time it takes to find the determinant of a (n-1)x(n-1) matrix
Since the arithmetic operation required here are just addition, multiplication and subtraction, the computation time could be crudely estimated as 4Tn!e for large n, where T is the clock cycle time and we assume that an addition or a multiplication or a subtraction each use 4 clock cycle times. Does it match?
For a 3.00 GHz machine, T={1}/({3 \times 10^9}) seconds to give an approximate time for a 12×12 matrix determinant calculation to be 4 \times {1}/{(3 \times 10^9)} \times 12! e = 1.736 seconds. It is not even of similar order. Many items go into calculating CPU time for a numerical algorithm, but to do a comparative analysis, these calculations are quite helpful.
This post is brought to you by
- Holistic Numerical Methods Open Course Ware:
- Numerical Methods for the STEM undergraduate at http://nm.MathForCollege.com;
- Introduction to Matrix Algebra for the STEM undergraduate at http://ma.MathForCollege.com
- the textbooks on
- the Massive Open Online Course (MOOCs) available at