Category: Binary conversions

A Floating Point Question Revisited

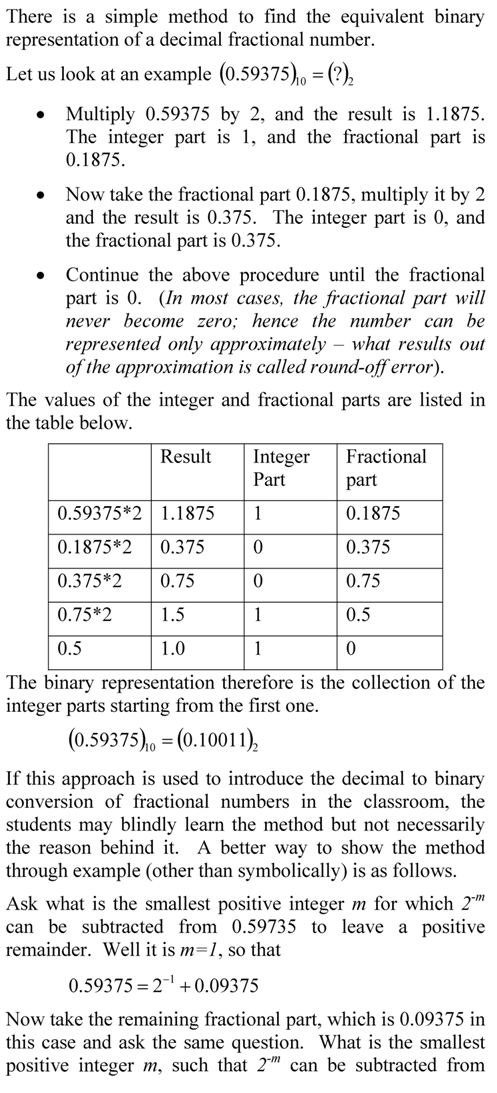
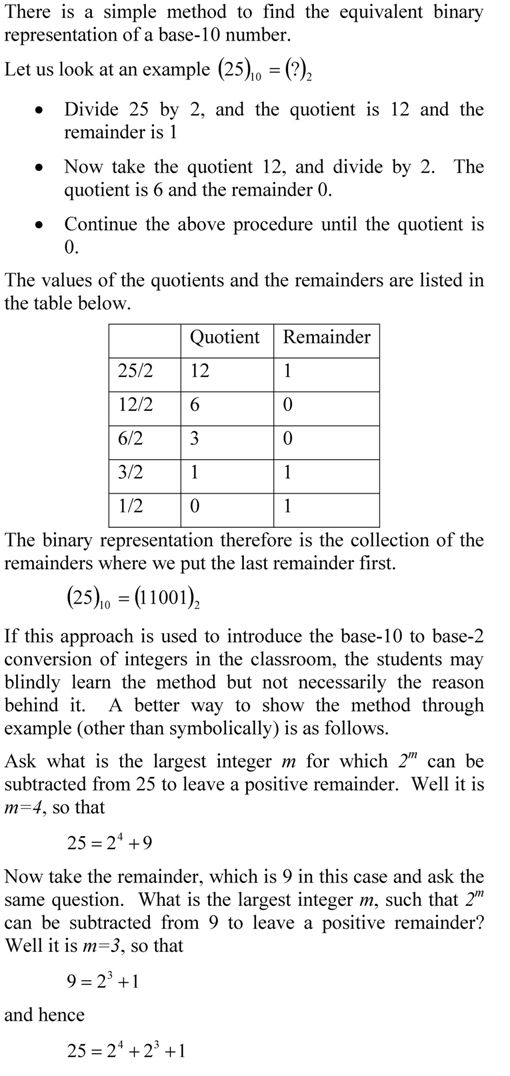
QUESTION: A machine stores floating point numbers in 7-bit word. The first bit is stored for the sign of the number, the next three for the biased exponent and the next three for the magnitude of the mantissa. You are asked to represent 33.35 in the above word. The error you will get in this case would be
(A) underflow
(B) overflow
(C) NaN
(D) No error will be registered

The solution to problem is given here.

However a student asked me a follow up question, and here is the answer.

QUESTION: I was doing the multiple choice question and I am having trouble understanding it. I looked at the solution but I am having trouble still. I began by turning 33.35 into binary and i get 100001.01011. I just am having trouble putting it into the format. The max exponent value is 4 in this case but in the solutions it says you need 5. Maybe I do not understand what underflow and over flow is exactly.

ANSWER: The solution is given as you have pointed out.

The binary number in fixed format needs to be converted to floating point format. That would be 100001.01011=1.0000101011*2^5 as you move the radix point by 5 places to the left.  We move that 5 places as it gives us only one non-zero digit now to the left of the radix point.  This is no different from the procedure you use for converting a decimal format to scientific format for base-10 numbers.

Now all floating point formats have an upper limit of number it can represent.  Since the biased exponent has 3 bits, the biased exponent that can be represented is from 0 to 7, which means the unbiased exponent that can be represented is from -3 to 4 (biasing by +3, and unbiasing by -3).  But since we need to represent an unbiased exponent of 5, it cannot be done.  The maximum unbiased exponent that can be represented is 4.  So the number is larger than the one that can be represented.  If you put 32 ounces of water in a 24-ounce cup, we say that the water overflowed.  In this case, the number will overflow as it is more than it can handle.

You can see this in a different way as follows (looking at a solution a different way; that always helps the brain and your long-term memory).

The maximum number you can represent in binary for the given 7-bit word is 0111111 and that translates to (1.111)2*2^(111)2 which in base 10 is equivalent to (1.875)*2^(7-3)=30 (the 3 is used for unbiasing the exponent).  Hence, 33.35 would overflow, just like when you put  32 ounces of water in a 24-ounce cup.

_____________________________________________________

This post is brought to you by

Largest integer that can be represented in a n-bit integer word

To find the largest integer in base-10 that can be represented in an n-bit integer word, let’s do this inductively.

  • If you have 3 bit-word, the highest number is (111) of base-2 which is 7 (1*2^2+1*2^1+1*2^0) of base-10,
  • If you have 4 bit-word, the highest number is (1111) of base-2 which is 15 (1*2^3+1*2^2+1*2^1+1*2^0) of base-10,
  • if you have 5 bit-word, the highest number is (11111) of base-2 which is 31 (1*2^4+1*2^3+1*2^2+1*2^1+1*2^0) of base-10. 

There is a trend here: 3 bit-word stores a maximum number of 7 (2^3-1), 4-bit word stores a maximum of 15 (2^4-1), 5 bit-word store a maximum number of 31 (2^5-1), and so on.   This means that the maximum number stored in n-bit word stores a maximum number of 2^n-1. 

We can derive the maximum number by knowing that the maximum base-10 number in a n-bit word is the summation series:
1*2^(n-1)+1*2^(n-2)+………+1×2^0. 
This is a geometric progression series.  The formula for the sum of a geometric series
        a+ar+ar^2+…+a*r^n =a*(1-r^(n+1))/(1-r), r ≠ 1,
Hence,
       1*2^(n-1)+1*2^(n-2)+………+1×2^0=1*(1-2^(n))/(1-2)=2^n-1 _____________________________________________________________

This post is brought to you by Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.mathforcollege.com, the textbook on Numerical Methods with Applications available from the lulu storefront, the textbook on Introduction to Programming Concepts Using MATLAB, and the YouTube video lectures available at http://nm.mathforcollege.com/videos.  Subscribe to the blog via a reader or email to stay updated with this blog. Let the information follow you.

A Wolfram demo on converting a decimal number to floating point binary representation

Here is another Wolfram demo. This one converts a decimal number to a floating point binary representation.  To play with the demo, download the free CDF player first.
 
The total number of bits used for the representation =
       one bit for the sign of the number +
       one bit for the sign of the exponent +
       number of bits for the exponent +
       number of bits for the mantissa +
       As an example, how would 54.75 be represented in a 9-bit register where the first bit is used for the sign of the number, second bit is used for sign of exponent, next three bits are used for the exponent, and the last four bits are used for the mantissa?
Both the number and the exponent are positive. 
As the number is normalized to lie between 1 and 2 (the interval being half-closed at the bottom and half-open at the top), the leading binary digit is always 1. So we do not actually use it in the representation of the mantissa. Hence the mantissa bits are 1011. Moreover the exponent bits are 101, the sign of the number bit is 0, and the sign of the exponent bit is 0.
Therefore the representation is .
 

Reference: Floating Point Representation

This post is brought to you by

Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.mathforcollege.com, the textbook on Numerical Methods with Applications available from the lulu storefront, the textbook on Introduction to Programming Concepts Using MATLAB, and the YouTube video lectures available at http://nm.mathforcollege.com/videos.  Subscribe to the blog via a reader or email to stay updated with this blog. Let the information follow you.

Converting large numbers into floating point format by hand

__________________________________________________

This post is brought to you by Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.mathforcollege.com, the textbook on Numerical Methods with Applications available from the lulu storefront, and the YouTube video lectures available at http://nm.mathforcollege.com/videos and http://www.youtube.com/numericalmethodsguy

Subscribe to the blog via a reader or email to stay updated with this blog. Let the information follow you.

A better way to show conversion of decimal fractional number to binary

This post is brought to you by Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.mathforcollege.com, the textbook on Numerical Methods with Applications available from the lulu storefront, and the YouTube video lectures available at http://www.youtube.com/numericalmethodsguy.  

Subscribe to the blog via a reader or email to stay updated with this blog. Let the information follow you.

A better way to show decimal to binary conversion

Decimal to binary conversion of an integer
Decimal to binary conversion of an integer

This post is brought to you by Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.mathforcollege.com.

An abridged (for low cost) book on Numerical Methods with Applications will be in print (includes problem sets, TOC, index) on December 10, 2008 and available at lulu storefront.

Subscribe to the blog via a reader or email to stay updated with this blog. Let the information follow you.