If you are solving a set of simultaneous linear equations, LU Decomposition method (involving forward elimination, forward substitution and back substitution) would use more computational time than Gaussian elimination (involving forward elimination and back substitution, but NO forward substitution).
So why use and waste time talking about LU Decomposition?
Because, LU Decomposition is computationally more efficient than Gaussian elimination when we are solving several sets of equations with the same coefficient matrix but different right hand sides. Case in point is when you are finding the inverse of a matrix [A]. If one is trying to find the inverse of nxn matrix, then it implies that one needs to solve n sets of simultaneous linear equations of [A][X]=[C] form with the n right hand sides [C] being the n columns of the nxn identity matrix, while the coefficient matrix [A] stays the same.
The computational time taken for solving a single set of n simultaneous linear equations is as follows:
- Forward elimination: Proportional to
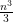
- Back substitution: Proportional to

- Forward substitution: Proportional to

So for LU decomposition method used to find the inverse of a matrix, the computational time is proportional to \frac{n^3}{3}+n( \frac{n^2}{2}+\frac{n^2}{2})=\frac{4n^3}{3}. Remember that the forward elimination only needs to be done only once on [A] to generate the L and U matrices for the LU decomposition method. However the forward and back substitution need to be done n times.
Now for Gaussian Elimination used to find the inverse of a matrix, the computational time is proportional to n \frac{n^3}{3} +n \frac{n^2}{2}=\frac{n^4}{3}+\frac{n^3}{2}. Remember that both the forward elimination and back substitution need to be done n times.
Hence for large n, for LU Decomposition, the computational time is proportional to \frac{4n^3}{3}, while for Gaussian Elimination, the computational time is proportional to  . So for large n, the ratio of the computational time for Gaussian elimination to computational for LU Decomposition is {\frac{n^4}{3}}/{\frac{4n^3}{3}}=\frac{n}{4}
. So for large n, the ratio of the computational time for Gaussian elimination to computational for LU Decomposition is {\frac{n^4}{3}}/{\frac{4n^3}{3}}=\frac{n}{4}
As an example, to find the inverse of a 2000×2000 coefficient matrix by Gaussian Elimination would take n/4=2000/4=500 times the time it would take to find the inverse by LU Decomposition.
So are you convinced now why we use LU Decomposition in certain cases? For textbook notes on this issue, examples of LU Decomposition to solve a set of equations, and finding inverse of a matrix using LU Decomposition, click here.
Reference: Numerical Methods for the STEM Undergraduate, http://nm.mathforcollege.com/topics/lu_decomposition.html
This post brought to you by Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.mathforcollege.com