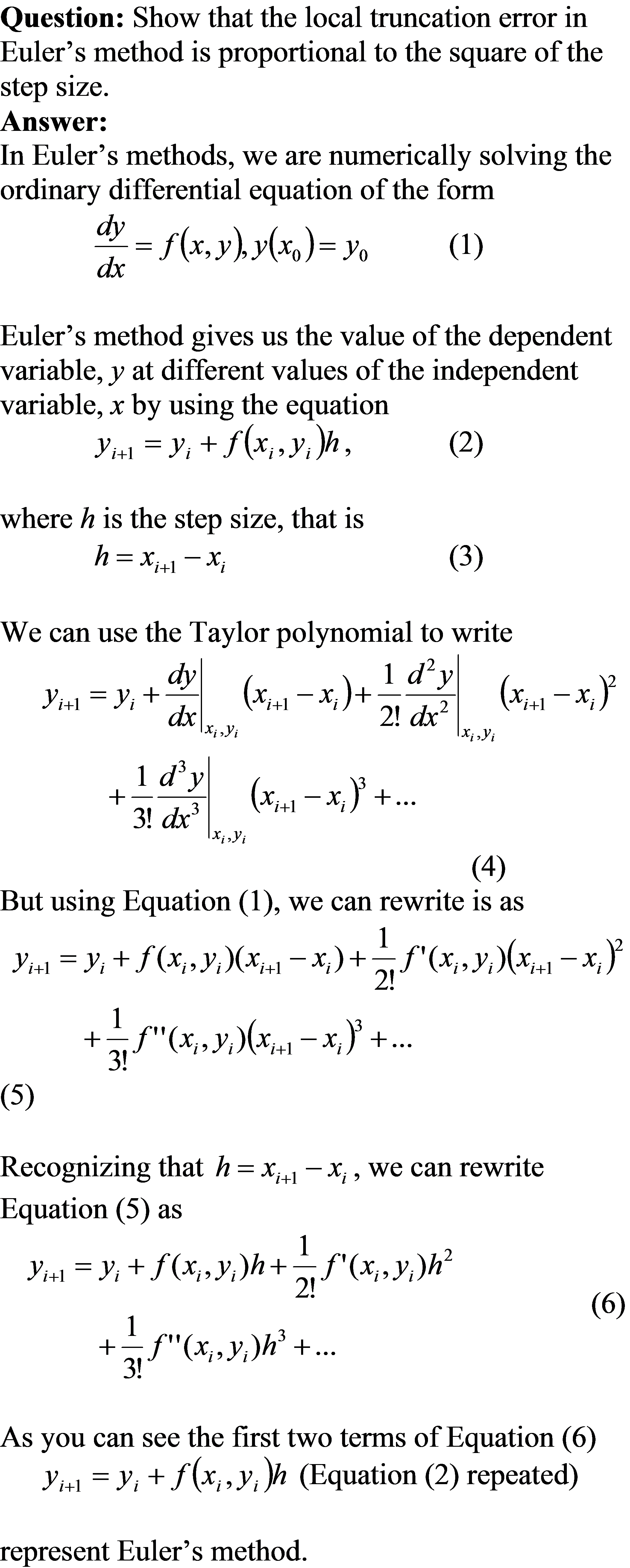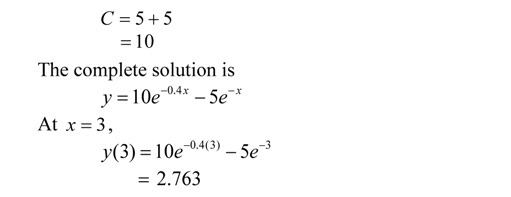Tag: ordinary differential equation

Solution to ordinary differential equations posed as definite integral

This blog is an example to show the use of second fundamental theorem of calculus in posing a definite integral as an ordinary differential equation.  This plays a prominent role in showing how we can use numerical methods of ordinary differential equations to conduct numerical integration.

This post is brought to you by

Local truncation error is approximately proportional to square of step size in Euler’s method

Question: Show that the local truncation error in Euler’s method is proportional to the square of the step size.

euler_truncation_local_pic1euler_truncation_local_pic2

This post is brought to you by

Example: Solving a first order ODE by Laplace transforms

I have a audiovisual digital lecture on YouTube that shows the use of Euler’s method to solve a first order ordinary differential equation (ODE).  To show the accuracy of Euler’s method,  I compare the approximate answer to the exact answer.  A YouTube viewer asked me: How did I get the exact answer?

In this blog, I use the Laplace transform technique to find the exact answer to the ODE.  In a previous blog, I showed how to find the exact answer to the ODE by the classicial solution technique.

Solving First Order Linear ODE by Laplace Transform Solution TechniqueSolving First Order Linear ODE by Laplace Transform Solution Technique

The pdf file of the solution is also available.

Classical Solution Technique to Solve a First Order ODE

I have a audiovisual digital lecture on YouTube that shows the use of Euler’s method to solve a first order ordinary differential equation (ODE).  To show the accuracy of Euler’s method,  I compare the approximate answer to the exact answer.  A YouTube viewer asked me: How did I get the exact answer?

In this blog, I use the classical solution technique to find the exact answer to the ODE.  In a previous blog, I showed how to find the exact answer to the ODE by the integrating factor method.

Solving First Order Linear ODE by Classical Solution TechniqueSolving First Order Linear ODE by Classical Solution Technique

The pdf file of the solution is also available.

Example: Solving First Order Linear ODE by Integrating Factor

I have a audiovisual digital lecture on YouTube that shows the use of Euler’s method to solve a first order ordinary differential equation (ODE).  To show the accuracy of Euler’s method,  I compare the approximate answer to the exact answer.  A YouTube viewer asked me: How did I get the exact answer?

In this blog, I use the integrating factor method to find the exact answer, because that is the method the viewer was using to solve the ODE exactly.  So here it is and in two future blogs, I will show the same example being solved by 1) Laplace transforms and 2) the classical (complementary + particular) solution techniques.
Solving First Order Linear ODE by Integrating Factor
Solving First Order Linear ODE by Integrating Factor

The pdf file of the solution is also available.

This post is brought to you by

Subscribe to the blog via a reader or email to stay updated with this blog. Let the information follow you.

Comparing Runge-Kutta 2nd order methods

Many a times, students ask me

Which of the Runge-Kutta 2nd order methods gives the most accurate answer to solving a first order ODE?

dy/dx=f(x,y), y(0)=y0

There is no direct answer, although Ralston’s method gives a minimum bound for the truncation error (Ralston, A., Runge-Kutta Methods with Minimum Error Bounds, Match. Compu., Vol 16, page 431, 1962).

They also ask me if using the first three terms of the Taylor series would give a more accurate answer if we calculate f^{\prime}(x,y) symbolically.

The equations for the four methods are given below

Here is the comparison graph for

dy/dx=sin(5*x)-0.4*y, y(0)=5

with

step size of h=1.1

and

step size of h=0.55

This post is brought to you by Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.mathforcollege.com

Subscribe to the blog via a reader or email to stay updated with this blog. Let the information follow you.