For example, $latex \int_{a}^{infinity} e^{-x} dx $ is an improper integral which can be calculated exactly as $latex e^{-a}$.
Can we solve this integral by multiple segment Trapezoidal rule when we already know that the upper limit is infinity?
Yes, we can solve it in spite of the upper limit being infinity. We first need to make a change of variables such as $latex t=\frac{1}{x}$, then $latex dx=-\frac{1}{t^2}dt$ giving $latex \int_{1/a}^{0} e^{-1/t} (-1/t^2) dt $
But even for this integral we have issues as the integrand gives division by zero problems at t=0 (although the limit itself is zero at t=0).
The MATLAB program that can be downloaded at http://nm.mathforcollege.com/blog/trapezoidal_improper.m (better to download it as the single quotes do not translate well with matlab editor) shows that we get accurate results for transformed integral with 256 segments.
% Simulation : Can I use Trapezoidal rule for an improper integral?
% Language : Matlab 2007a
% Authors : Autar Kaw, http://nm.mathforcollege.com
% mfile available at
% http://nm.mathforcollege.com/blog/trapezoidal_improper.m
% Last Revised : July 15, 2008
% Abstract: This program shows use of multiple segment Trapezoidal
% rule to integrate exp(-x) from x=a to infinity, where a>0.
clc
clear all
disp(‘This program shows the convergence of getting the value of ‘)
disp(‘an improper integral using multiple segment Trapezoidal rule’)
disp(‘Author: Autar K Kaw. autarkaw.wordpress.com’)
%INPUTS. If you want to experiment, these are the only variables
% you should and can change.
% a = Lower limit of integration
a=1/2;
fprintf(‘\nFinding the integral of exp(-x) from a to infinity where a=%g’,a)
% SIMULATION
syms x
% integrand exp(-x)
f=exp(-x);
valexact=double(int(f,x,a,inf));
fprintf(‘\n\nExact value of integral = %f’,valexact)
disp( ‘ ‘)
% Transformed integrand by change of variables
ft=inline(‘exp(-1/t)*(-1/t^2)’);
% Limits of integration
at=1/a;
b=0;
%finding value of the integral using 16, 32, 64, 128 and 256 segments
for k=4:1:8
n=2^k;
h=(b-at)/n;
sum=0;
for i=1:1:n-1
sum=sum+ft(at+i*h);
end
% See how f(b) is not added as f(b)=infinity. But
% using a different value of the function at one point or
% finite number of points does not change the value of the
% integral. We are substituting f(b)=0
sum=2*sum+ft(at)+0;
sum=(b-at)/(2*n)*sum;
fprintf(‘\nApproximate value of integral =%f with %g segments’,sum,n)
end
disp(‘ ‘)
This program shows the convergence of getting the value of
an improper integral using multiple segment Trapezoidal rule
Author: Autar K Kaw. autarkaw.wordpress.com
Finding the integral of exp(-x) from a to infinity where a=0.5
Exact value of integral = 0.606531
Approximate value of integral =0.605971 with 16 segments
Approximate value of integral =0.606496 with 32 segments
Approximate value of integral =0.606521 with 64 segments
Approximate value of integral =0.606528 with 128 segments
Approximate value of integral =0.606530 with 256 segments
Published with MATLAB® 7.3
Now someone may rightly point out that it works well because the limit of the integrand is zero at the lower limit of integration for the above mentioned integral.
So go ahead, modify the program for doing this improper integral $latex \int_{0}^{4} \frac{1}{\sqrt {x}} dx $ and see how well it works. In this case the integrand is singular at $latex x=0$ and one would have to assume the function to be a number other than infinity at $latex x=0$ for applying the multiple segment Trapezoidal rule.
How many segments do you need to get an accurate answer for this integral?
_____________________________________________________
This post is brought to you by Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.mathforcollege.com
Subscribe to the blog via a reader or email to stay updated with this blog. Let the information follow you.
 Exercises assigned to the students:
Exercises assigned to the students:

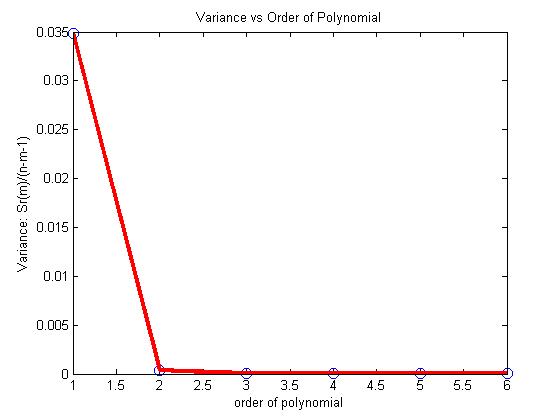
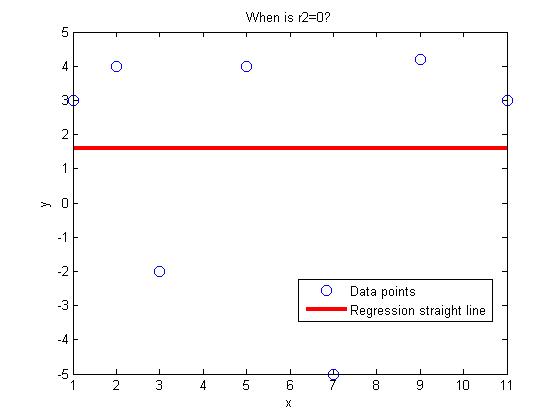
 In this experiment, we find the length of two curves generated from the same points – one curve is a polynomial interpolant and another one is a spline interpolant.
In this experiment, we find the length of two curves generated from the same points – one curve is a polynomial interpolant and another one is a spline interpolant.