Many a times, you may not have the privilege or knowledge of the physics of the problem to dictate the type of regression model. You may want to fit the data to a polynomial. But then how do you choose what order of polynomial to use.
Do you choose based on the polynomial order for which the sum of the squares of the residuals, Sr is a minimum? If that were the case, we can always get Sr=0 if the polynomial order chosen is one less than the number of data points. In fact, it would be an exact match.
So what do we do? We choose the degree of polynomial for which the variance as computed by
Sr(m)/(n-m-1)
is a minimum or when there is no significant decrease in its value as the degree of polynomial is increased. In the above formula,
Sr(m) = sum of the square of the residuals for the mth order polynomial
n= number of data points
m=order of polynomial (so m+1 is the number of constants of the model)
Let’s look at an example where the coefficient of thermal expansion is given for a typical steel as a function of temperature. We want to relate the two using polynomial regression.
|
Temperature |
Instantaneous Thermal Expansion |
|
oF |
1E-06 in/(in oF) |
|
80 |
6.47 |
|
40 |
6.24 |
|
0 |
6.00 |
|
-40 |
5.72 |
|
-80 |
5.43 |
|
-120 |
5.09 |
|
-160 |
4.72 |
|
-200 |
4.30 |
|
-240 |
3.83 |
|
-280 |
3.33 |
|
-320 |
2.76 |
If a first order polynomial is chosen, we get
$latex alpha=0.009147T+5.999$, with Sr=0.3138.
If a second order polynomial is chosen, we get
$latex alpha=-0.00001189T^2+0.006292T+6.015$ with Sr=0.003047.
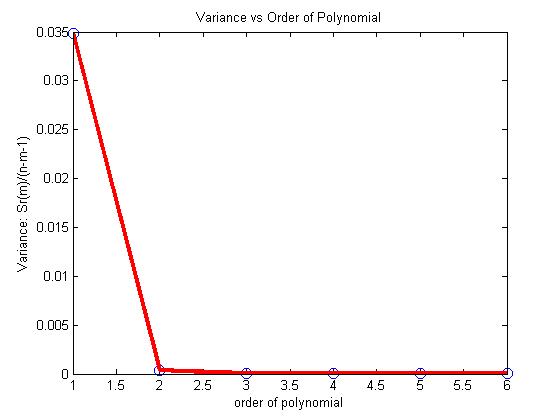
Below is the table for the order of polynomial, the Sr value and the variance value, Sr(m)/(n-m-1)
|
Order of polynomial, m |
Sr(m) |
Sr(m)/(n-m-1) |
|
1 |
0.3138 |
0.03486 |
|
2 |
0.003047 |
0.0003808 |
|
3 |
0.0001916 |
0.000027371 |
|
4 |
0.0001566 |
0.0000261 |
|
5 |
0.0001541 |
0.00003082 |
|
6 |
0.0001300 |
0.000325 |
So what order of polynomial would you choose?
From the above table, and the figure below, it looks like the second or third order polynomial would be a good choice as very little change is taking place in the value of the variance after m=2.
This post is brought to you by Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.mathforcollege.com
Subscribe to the feed to stay updated and let the information follow you.
Hi, how exactly do you calculate Sr? I read your definition of it several times but still clues. Please let me know. Thanks.
Hi, how exactly do you calculate Sr? I read your definition of it several times but still clues. Please let me know. Thanks.
Hello Ken:
To find what Sr is about http://numericalmethods.eng.usf.edu/mws/gen/06reg/mws_gen_reg_txt_straightline.pdf
To see how Sr is calculated for this example, go to page 7 of http://numericalmethods.eng.usf.edu/mws/gen/06reg/mws_gen_reg_txt_nonlinear.pdf
Hello Ken:
To find what Sr is about http://numericalmethods.eng.usf.edu/mws/gen/06reg/mws_gen_reg_txt_straightline.pdf
To see how Sr is calculated for this example, go to page 7 of http://numericalmethods.eng.usf.edu/mws/gen/06reg/mws_gen_reg_txt_nonlinear.pdf
Very nice article but I cannot seam to know how to interpret the following sentence:
We choose the degree of polynomial for which the variance as computed by
Sr(m)/(n-m-1)
is a minimum or when there is no significant decrease in its value as the degree of polynomial is increased
So, what does “significant decrease” mean? Is it statistical significance test? Or you just set a threshold, say 0.001, and choose the order when the change in the Sr(m)/(n-m-1) drops below this threshold?
Could you help me out on this issue?
Thanks!
Very nice article but I cannot seam to know how to interpret the following sentence:
We choose the degree of polynomial for which the variance as computed by
Sr(m)/(n-m-1)
is a minimum or when there is no significant decrease in its value as the degree of polynomial is increased
So, what does “significant decrease” mean? Is it statistical significance test? Or you just set a threshold, say 0.001, and choose the order when the change in the Sr(m)/(n-m-1) drops below this threshold?
Could you help me out on this issue?
Thanks!
There is no rule of thumb that I know of. If there is a minimum at a low order of polynomial, that is an indication of the optimum polynomial as well. If there is any threshold, it should be a relative number.
Thanks for your answer!
I am working to find an algorithmic/automatic way of predicting the order of the polynomial.
But with not much luck!
However I found ways to predict the order of the polynomial and accept that it can overestimate the true order… it can do that with 83% accuracy.
I’m still crunching numbers!
This is very nice technique, but I cannot understand the meaning of the denominator ‘n-m-1’.
Is it a weighting?
Thanks!
This is very nice technique, but I cannot understand the meaning of the denominator ‘n-m-1’.
Is it a weighting?
Thanks!
Hi, this is good article.
However I cannot understand the meaning of (n-m-1).
Is this a weighting?
Also, is there any reference of this article?
Please tell me it.
Thank you.
Hi, this is good article.
However I cannot understand the meaning of (n-m-1).
Is this a weighting?
Also, is there any reference of this article?
Please tell me it.
Thank you.
Yes, it is weighting. If n=m+1, then Sr=0. So it weights reduction is Sr and increase in polynomial order.
Hi, thank you for this informative article. However, I don’t understand why n-m-1 is used as the denominator instead of n-1.
Hi, thank you for this informative article. However, I don’t understand why n-m-1 is used as the denominator instead of n-1.
Rewrite n-m-1 as n-(m+1). The numerator is Sr for a polynomial of order m. So when n=m+1, then Sr=0. So as m increases, Sr, and n-(m+1) both decrease. And since we want something that is optimum, we give them equal weight. Plot n-m-1 vs m and Sr vs m separately to see what happens.
Why would I want to provide equal weightage to n-m-1? Isn’t the Sr satisfactory enough?
Why would I want to provide equal weightage to n-m-1? Isn’t the Sr satisfactory enough?
If Sr is given all the weight, then the optimum order of polynomial m is n-1. This is the case where the polynomial goes through all the data points and Sr=0. But regression is all about finding a simplified curve to represent the data.
That’s a great note. I just want to ask on the following:
Can the optimal degree be determined by just looking at the Peaks and Troughs?
I’m asking because what if I don’t have software to do so, and I’m just running out of time?
I tried this method but the variance behaviour is so confusing. From order one to order ten, the variance just go up and down and up and down. Can you advise me on this?
That’s a great note. I just want to ask on the following:
Can the optimal degree be determined by just looking at the Peaks and Troughs?
I’m asking because what if I don’t have software to do so, and I’m just running out of time?
I tried this method but the variance behaviour is so confusing. From order one to order ten, the variance just go up and down and up and down. Can you advise me on this?
You can do this in software like excel, etc. Learn VBA for excel. No shortcuts. You can use free software like Python, etc.
Hello Autar Kaw!
I have one question about using the “sum of squared residuals” as a criterion for finding the optimal order. When we increase the order of the polynomial, we will always decrease the sum of the squares of the residuals until we get an overtrained model (the polynomial will cross all the training points). Is this a way to retrain? And how can I tell when I need to stop?
That is why n-(m+1) is used to compensate for the decreasing residual. Keep in mind, this is just a criterion that makes sense. Its validity is not proven.
Hello Autar Kaw!
I have one question about using the “sum of squared residuals” as a criterion for finding the optimal order. When we increase the order of the polynomial, we will always decrease the sum of the squares of the residuals until we get an overtrained model (the polynomial will cross all the training points). Is this a way to retrain? And how can I tell when I need to stop?
That is why n-(m+1) is used to compensate for the decreasing residual. Keep in mind, this is just a criterion that makes sense. Its validity is not proven.
What about this situation:
There is a 5% fall in variance from X^1 to X^2,but there is a 43% fall in variance from second to third order.
I’m using 10 observations to find the right order in order to explain.
Should I just focus only on first half (first to fifth order) and analyze the behaviour of their variances which is from your formula SSR/n-m-1?
Please advise.
Thanks
Unless you have a better criterion, SSR/(n-m-1) seems to be a good objective function. How much fall you look for in this number is mostly in the eye of the beholder as we are not looking for a minimum.
What about this situation:
There is a 5% fall in variance from X^1 to X^2,but there is a 43% fall in variance from second to third order.
I’m using 10 observations to find the right order in order to explain.
Should I just focus only on first half (first to fifth order) and analyze the behaviour of their variances which is from your formula SSR/n-m-1?
Please advise.
Thanks
Unless you have a better criterion, SSR/(n-m-1) seems to be a good objective function. How much fall you look for in this number is mostly in the eye of the beholder as we are not looking for a minimum.
Hi Autar,
I enjoyed reading your article but I do have a few questions:
* When playing around a bit with your selection criterion I noticed that quite often a 3rd or 4th order polynomial was prefered when I generated my random data based on a 2nd order polynomial because the variance for those orders was a slightly lower than for the 2nd order polynomial. In your article you mention that once there is no significant improvement anymore you’ve found your optimal order of your polynomial which I understand but find difficult to implement given that it is quite vague. Nonetheless, I presume we could come up with a rule of thumb to define ‘significant’. However, that way the criterion becomes more and more subjective in my opinion. What’s your take on this?
* My first thought to tackle the same problem was to simply use the widely known BIC criterion. When playing around with some dummy data this seemed to be a bit more robust. Apart from that it is also less subjective given that no additional definition for ‘significant’ improvement is required. Do you see any shortcoming in using BIC?
Thanks a lot for your article!
Arno
Hi Autar,
I enjoyed reading your article but I do have a few questions:
* When playing around a bit with your selection criterion I noticed that quite often a 3rd or 4th order polynomial was prefered when I generated my random data based on a 2nd order polynomial because the variance for those orders was a slightly lower than for the 2nd order polynomial. In your article you mention that once there is no significant improvement anymore you’ve found your optimal order of your polynomial which I understand but find difficult to implement given that it is quite vague. Nonetheless, I presume we could come up with a rule of thumb to define ‘significant’. However, that way the criterion becomes more and more subjective in my opinion. What’s your take on this?
* My first thought to tackle the same problem was to simply use the widely known BIC criterion. When playing around with some dummy data this seemed to be a bit more robust. Apart from that it is also less subjective given that no additional definition for ‘significant’ improvement is required. Do you see any shortcoming in using BIC?
Thanks a lot for your article!
Arno