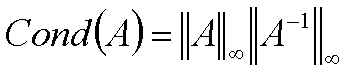A square matrix A is strictly diagonally dominant if for all rows the absolute value of the diagonal element in a row is strictly greater than than the sum of absolute value of the rest of the elements in that row.
In this posting, I show a MATLAB program that finds whether a square matrix is strictly diagonally dominant by using two different methods. These are academic ways to reinforce programming skills in a student.
The MATLAB program can be downloaded as a Mfile (better to download it, as single quotes from the web-post do not translate correctly with the MATLAB editor). The html file showing the mfile and the command window output is also available.
%% IS A GIVEN SQUARE MATRIX STRICTLY DIAGONALLY DOMINANT?
% Language : Matlab 2007a
% Authors : Autar Kaw
% Last Revised : November 25, 2008
% Abstract: This program shows you two ways of finding out
% if a square matrix is diagonally dominant. A square matrix is
% diagonally dominant if for all rows the absolute value of the
% diagonal element in a row is strictly greater than than the sum
% of absolute value of the rest of the elements in that row
clc
clear all
disp(‘This program shows you two ways of finding out’)
disp(‘if a square matrix is diagonally dominant. A square matrix is’)
disp(‘diagonally dominant if for all rows the absolute value of the’)
disp(‘diagonal element in a row is strictly greater than than the sum’)
disp(‘of absolute value of the rest of the elements in that row’)
disp(‘ ‘)
%% INPUTS
% The square matrix
A=[-12 1 -7 2;1 3.4 1.1 1.1; 1 0 -4.5 0;10 1 1 10];
disp (‘INPUTS’)
disp(‘Here is the square matrix’)
A
disp(‘ ‘)
%% FIRST SOLUTION
% This is based on finding for how many rows the condition
% the absolute value of the diagonal element in a row is
% strictly greater than than the sum of absolute value
% of the rest of the elements in that row.
%size gives how many rows and columns in the A matrix
rowcol=size(A);
n=rowcol(1);
% count = for how many rows is the inequality met that
% the absolute value of the diagonal element in a row is
% strictly greater than than the sum of absolute value
% of the rest of the elements in that row
count=0;
for i=1:1:n
sumrow=0;
for j=1:1:n
if i~=j
sumrow=sumrow+abs(A(i,j));
end
end
if abs(A(i,i))>sumrow
count=count+1;
end
end
disp(‘FIRST WAY’)
if count==n
disp(‘Matrix is strictly diagonal dominant’)
else
disp(‘Matrix is NOT strictly diagonal dominant’)
end
%% SECOND SOLUTION
% This is based on finding for if for any row the condition
% the absolute value of the diagonal element in a row is
% strictly greater than than the sum of absolute value
% of the rest of the elements in that row is NOT met
%size gives how many rows and columns in the A matrix
rowcol=size(A);
n=rowcol(1);
% flag = keeps track if the condition is not met
% flag = 1 if matrix is strictly diagonally dominant
% flag = 2 if matrix is not strictly diagonally dominant
% Assuming matrix is strictly diagonally dominant
flag=1;
for i=1:1:n
sumrow=0;
for j=1:1:n
if i~=j
sumrow=sumrow+abs(A(i,j));
end
end
% As soon as the condition is not met, it is not a strictly
% diagonally dominant matrix
if abs(A(i,i))<=sumrow
flag=2;
break;
end
end
disp(‘ ‘)
disp(‘SECOND WAY’)
if flag==1
disp(‘Matrix is strictly diagonal dominant’)
else
disp(‘Matrix is NOT strictly diagonal dominant’)
end
This post is brought to you by Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.mathforcollege.com and the textbook on Numerical Methods with Applications available from the lulu storefront.
Subscribe to the blog via a reader or email to stay updated with this blog. Let the information follow you.