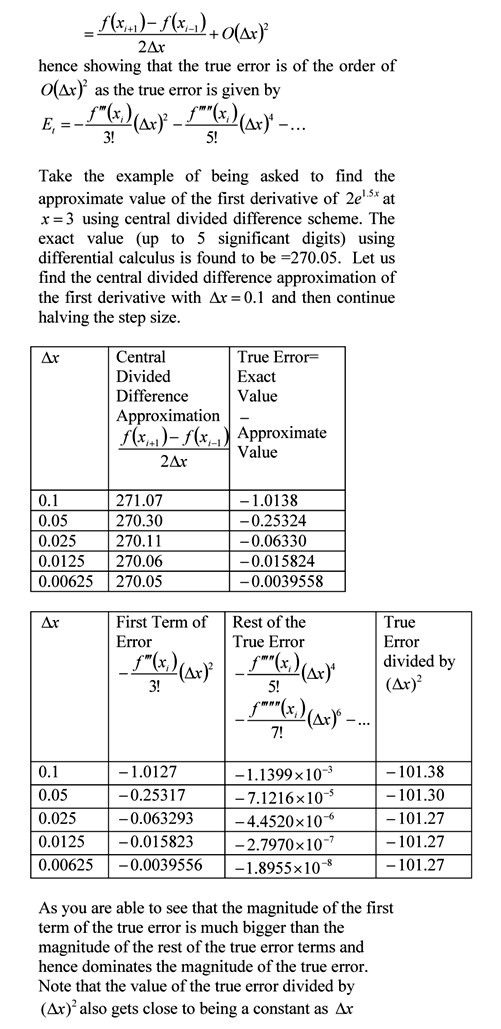
Many students are challenged to understand the nature of Big Oh in relating it to the order of accuracy of numerical methods. In this exercise, we are using the central divided difference approximation of the first derivative of the function to ease some of the mystery surrounding the Big Oh.


You can visit the above example by opening a pdf file.
This post is brought to you by Holistic Numerical Methods: Numerical Methods for the STEM undergraduate at http://nm.MathForCollege.com, the textbook on Numerical Methods with Applications available from the lulu storefront, the textbook on Introduction to Programming Concepts Using MATLAB, and the YouTube video lectures available at http://nm.MathForCollege.com/videos. Subscribe to the blog via a reader or email to stay updated with this blog. Let the information follow you.
Hi Mr. Kaw! I’ve been using the numeric methods material from mathoforcollege,com for my numerical methods course and wanted to thank you for taking the time to make it all so simple and easy to understand, please keep up the good work.
Hi Mr. Kaw! I’ve been using the numeric methods material from mathoforcollege,com for my numerical methods course and wanted to thank you for taking the time to make it all so simple and easy to understand, please keep up the good work.